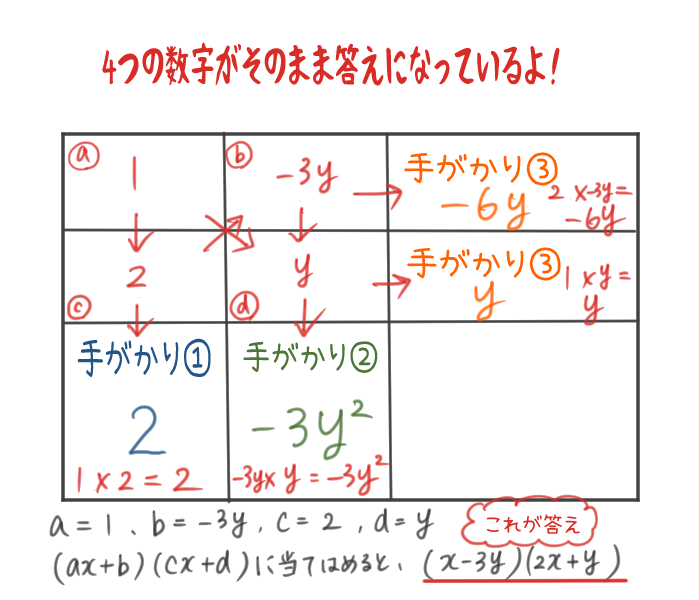
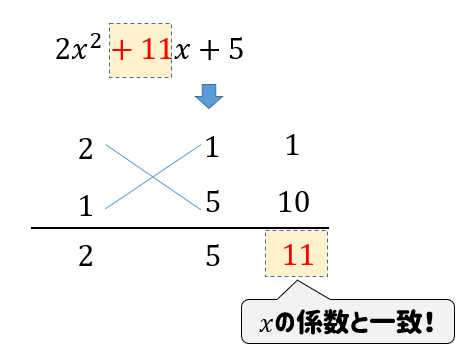
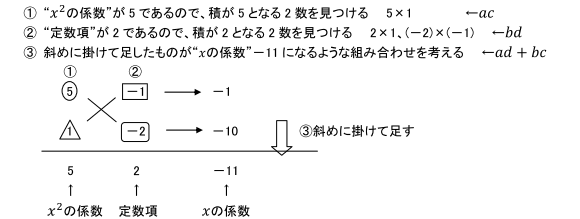
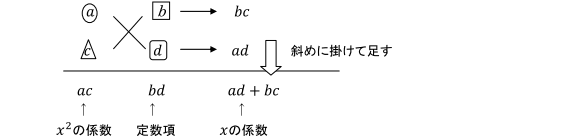
1:たすき掛けとは? まずは因数分解におけるたすき掛けとは何かについて解説します。 たすき掛けはイメージが非常に大切ですので、ぜひ本章でたすき掛けのイメージをしておきましょう! 例えば、 ax 2 bxc が (アxイ)(ウxエ) に因数分解できたとしましょう。 たすき掛け acx2(adbc)xbd=(axb)(cxd) と言われたって数字が大きくなったら困りません? 12x216x3とか。ぱっと思いつきませんよね? そんな時に「たすき掛け」という方法があります。 手順 ①x²の係数を〇× という積の形にして図のように縦に書きます。(とりあえずこの時点で〇と の組合せはの問題の因数分解(たすきがけ)についてですね。 解説 5 x 2 11 x 2☆は、 acx 2 ( ad bc ) x bd =( ax b )( cx d )を使って因数分解しますが、『たすきがけ』を使うとうまく a 、 b 、 c 、 d が見つかります。

たすき掛けで因数分解をするやり方を解説 これでたすき掛けに困らない
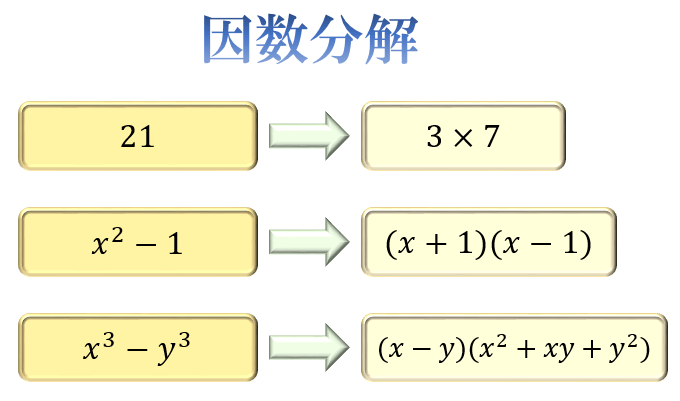
数1 因数分解 たすき掛け
数1 因数分解 たすき掛け-たすき掛け(応用)のポイントは! ① 次数に差がない複数の文字の2次式の因数分解の手順は、1 一つの文字について整理する! 2 定数項を1.題材名 因数分解(数学Ⅰ 第1章 数と式 第1節 整式 3 因数分解) 2.主眼 たすき掛けによる因数分解の意味がわかり,因数分解ができるようになる。 3.準備 パソコン,ワイヤレスパワーポインター,テレビ,プリント 4.学習過程



高一です 因数分解のこのたすき掛けのやり方って数が大きくなったらすご Yahoo 知恵袋
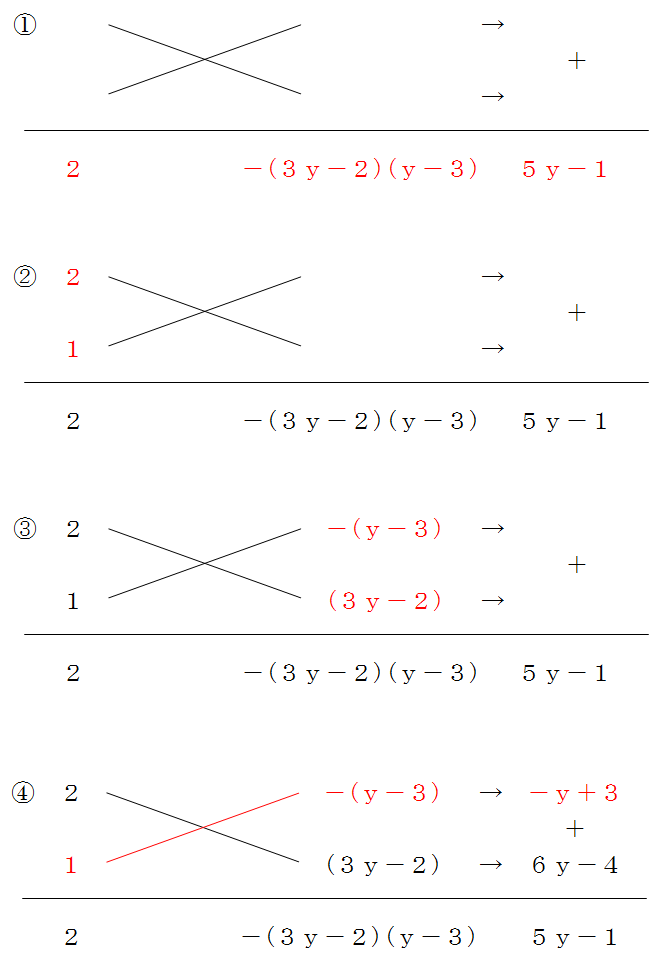
でも、アとイのどっちが正解かわかるかな? ここでいよいよ登場するのが たすきがけの計算 なんだ! たすきがけの計算 上の図では、xの係数が 「たして5」 になるというヒントを使っているよ。 2x×1=2x、x×3=3xをたすきのようにかけ算して2x+3x= 5x を導き出しているよね。 こうしてイの(2x+3)(x+1)が正解だとわかるんだ。 ポイントをまとめると次のたすき掛けの因数分解 \(3x^214x8=(x4)(3x2)\) この方程式をたすき掛けで因数分解しましょう。 \(x^2\)の係数と一番後ろの定数項に注目します。 今回ならば、 \(x^2\)の係数が3 、 定数項が8 です。 次に、積が3になる数の組と積が8になる数の組を考えます。 高校数学の代名詞?の1つ, たすき掛けの因数分解を書いておきます。次の展開公式の逆ですね。以下の乗法公式の逆, つまり, の因数分解のことです。この因数分解は以下のからくりを用いて完成させます。の係数を構成する2数を縦に
このように変形すると、「たすき掛け因数分解」として、掛けると 2 になる2つの数( 1 と 2 )および掛けると 3y 2 2y−1 となる2つの数(ここでは y も数字、係数として扱っているから y を含む式をたすき掛け因数分解とは x 2 の係数が1でない2次式を因数分解する一つの方法が,たすき掛け因数分解と呼ばれる方法である.たすき掛けの因数分解 第1章 数と式 §1 式の計算 12 整式の乗法 式の展開の工夫 p13 13 因数分解 たすき掛けの因数分解 p16 ※pp1415は各自で取り組むこと 1
適当な公式を用いて,次の式を因数分解せよ。 \ 10 次の式を因数分解せよ。 de d e de de d e \ de\ 11 次の式を因数分解せよ。 数学Ⅰ 数と式(因数分解) 演習プリント式の計算因数分解(たすき掛け) s 練習問題 3次の式を因数分解せよ。 D E D F D Eたすき掛けのポイントは! ① 2次の項の係数に何かいる式の因数分解は、たすき掛けを利用できないか疑おう! ② たすき掛けの手順は、12次




高校数学 たすきがけのコツ1 符号 映像授業のtry It トライイット



因数分解たすきがけの裏ワザ 教科書では教えてくれない たすき掛けを早く簡単にする方法 とは 教科書をわかりやすく通訳するサイト
保護中 1年生 数学Ⅰ 因数分解②たすき掛け 年5月22日 / カテゴリ 1年数学 , お知らせ / 作成者 NHD7541DAxumm47 このコンテンツはパスワードで保護されています。よって、 6x 2 +x-2=(2x-1)(3x+2) と因数分解される。 たすき掛けの計算を多少軽減する方法として、西元教善先生の裏技が参考になると思う。 (→ 参考:「指導者のためのたすき掛け」)数学I 授業プリント# 14, 年 組 号 氏名 1x2 − 2x − 24 を因数分解したい。 次の問いに答えよ。 ⑴ たし算すると−2 になり,かけ算すると−24 になる2 つの数を見つけよ。 (かけ算の方から考え た方が簡単です) 〈答〉 と ⑵ (1) よりx2 − 2x − 24 = x)(x) と因数分解できる。




数学 問題演習 たすき掛けを用いる因数分解 教科書より詳しい高校数学




たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ
1次式の因数分解は,共通因数でくくる変形があるだけですから,共通因数を考えます. (ab) x (ab) (a−b) = (ab) (xa−b) (答) この問題を a について整理しても間違いではありませんが,2次式の因数分解になるので次のようにやや複雑になります. a x たすき掛けのやり方はわかってもらえたと思います。 ここで「 なぜたすき掛けでうまく因数分解ができるの? 」という疑問について説明していきたいと思います。 そもそも、たすき掛けが何をやっているのかということを式で表すと以下のようになり <因数分解のやり方をこの1記事でマスター> 数学の計算や、問題を解いていく上で「基本中の基本」となる『因数分解』ですが、数Ⅲや数Ⅱbで点数が取れないことの根本原因が、 因数分解などの基礎事項であった、 ということは非常に多いのです。 ぜひこの記事をじっくり読んで、因数分解



たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com




たすきがけを使った因数分解 Youtube
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru だけど、因数分解にもじつは、 たすき掛け という解き方があるんだ。 今日は、この解き方を5ステップで解説していくよ。 よかったら参考にしてみてね。 たすき掛けの因数分解のやり方がわかる5つのステップ さっきもいったけど、高校数学(数i) 因数分解、基本編、たすき掛け編、応用編、3次式の公式編 みなさん、初めまして。 本講座を担当している葉一(はいち)と申します。 私は元塾講師なのですが、塾講師として勤務していた期間に何度も この言葉を耳にしました。



たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ
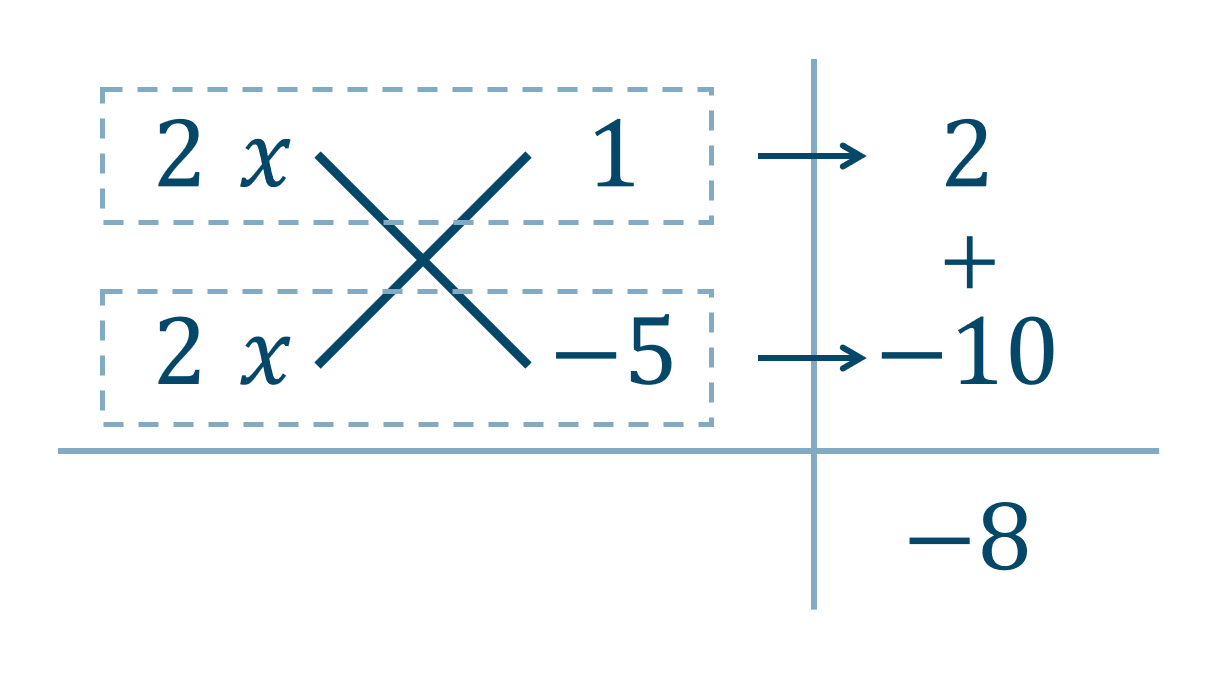



数学 問題演習 たすき掛けを用いる因数分解 教科書より詳しい高校数学
このように変形すると、「たすき掛け因数分解」として、掛けると 2 になる2つの数( 1 と 2 )および掛けると 3y 2 2y−1 となる2つの数(ここでは y も数字、係数として扱っているから y を含む式を考たすきがけによる因数分解 たすきがけとは,二次式を因数分解するための方法です。たすきがけを使って 3 x 2 − 10 x 8 3x^210x8 3 x 2 − 10 x 8 を因数分解してみましょう。 手順1 かけて 3 3 3 (二次の係数)になる2つの整数を適当に決めて左に縦に並べる なぜなら,2数を整数に限定したとき,「たして $1$ 」になる数 公式や2次方程式に頼らずこれを繰り返すことが,たすき掛けの因数分解に慣れる唯一の方法です。 ※余談ですが,因数分解は無限にありそうに思えて,因数分解された1次式の係数が1桁




たすきがけの仕方とは 因数分解を早くするコツを問題6選で解説します 遊ぶ数学




たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com
より、因数分解をすると\((2x1)(3x2)\)となります。 この仕組みがわかっても\(a,b,c,d\)に当たる数字をすぐに見つけにくいことがあります。 このとき\(ac、(adbc)、bd\)にあたる3つの数字に1以外 共通の約数はない ことが前提となっています。 因数分解のたすき掛け ではないでしょうか。 高校数学のレベルの高さを感じてしまいます(^^;) だけど、しっかりと練習を積むことで 誰だってスラスラと解けるようになっちゃいます! 今回の記事では、たすき掛けを使った因数分解の解き方を伝授。 因数分解(整理してたすき掛け) 因数分解せよ 6x 215y 2 xyx11y2 説明 次数が同じなのでどちらの文字に着目してもよい。 今回は、xについて降べきの順に整理する。 xを含まない部分の yの2次式を因数分解 する。 そして、たすき掛けの因数分解をする。
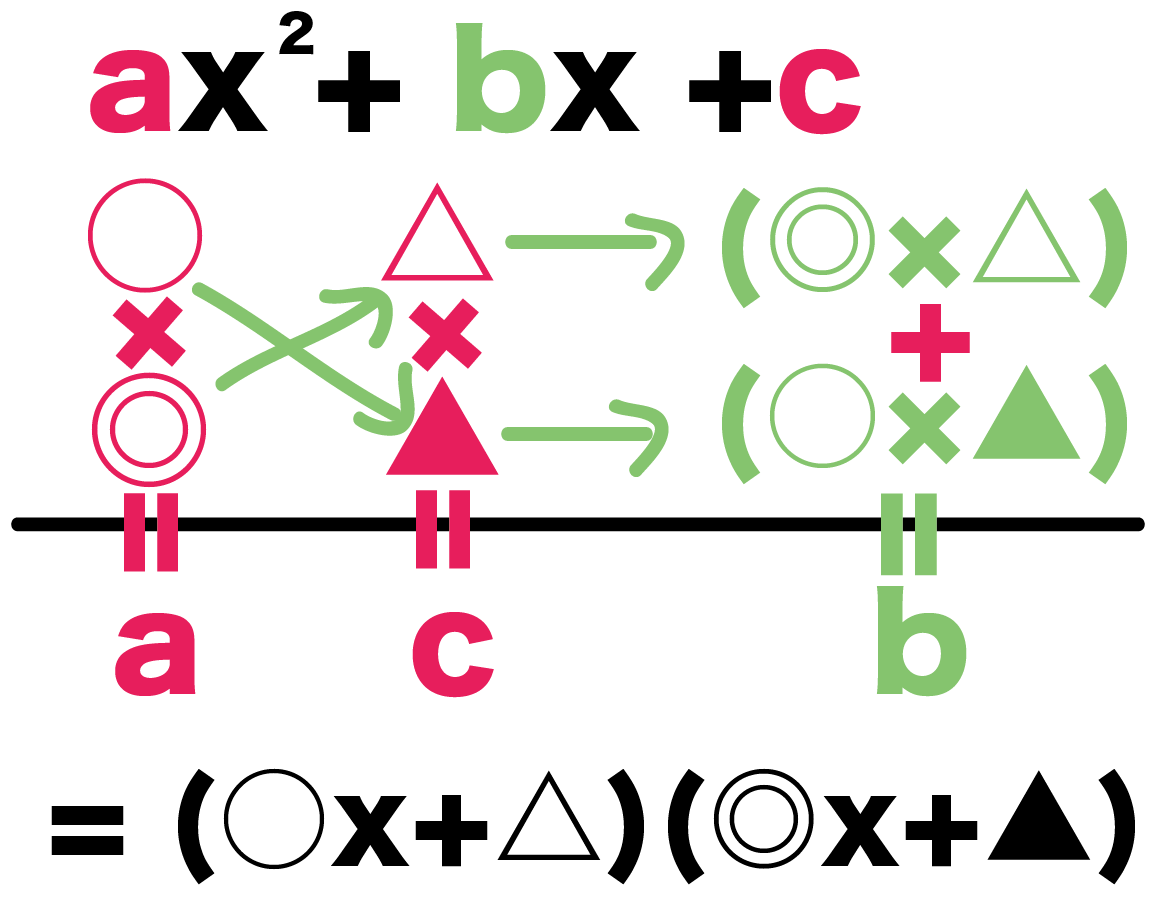



中学数学 たすき掛け因数分解のやり方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




数学 質問解答 高校生の因数分解 複雑な式のたすきがけ 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生
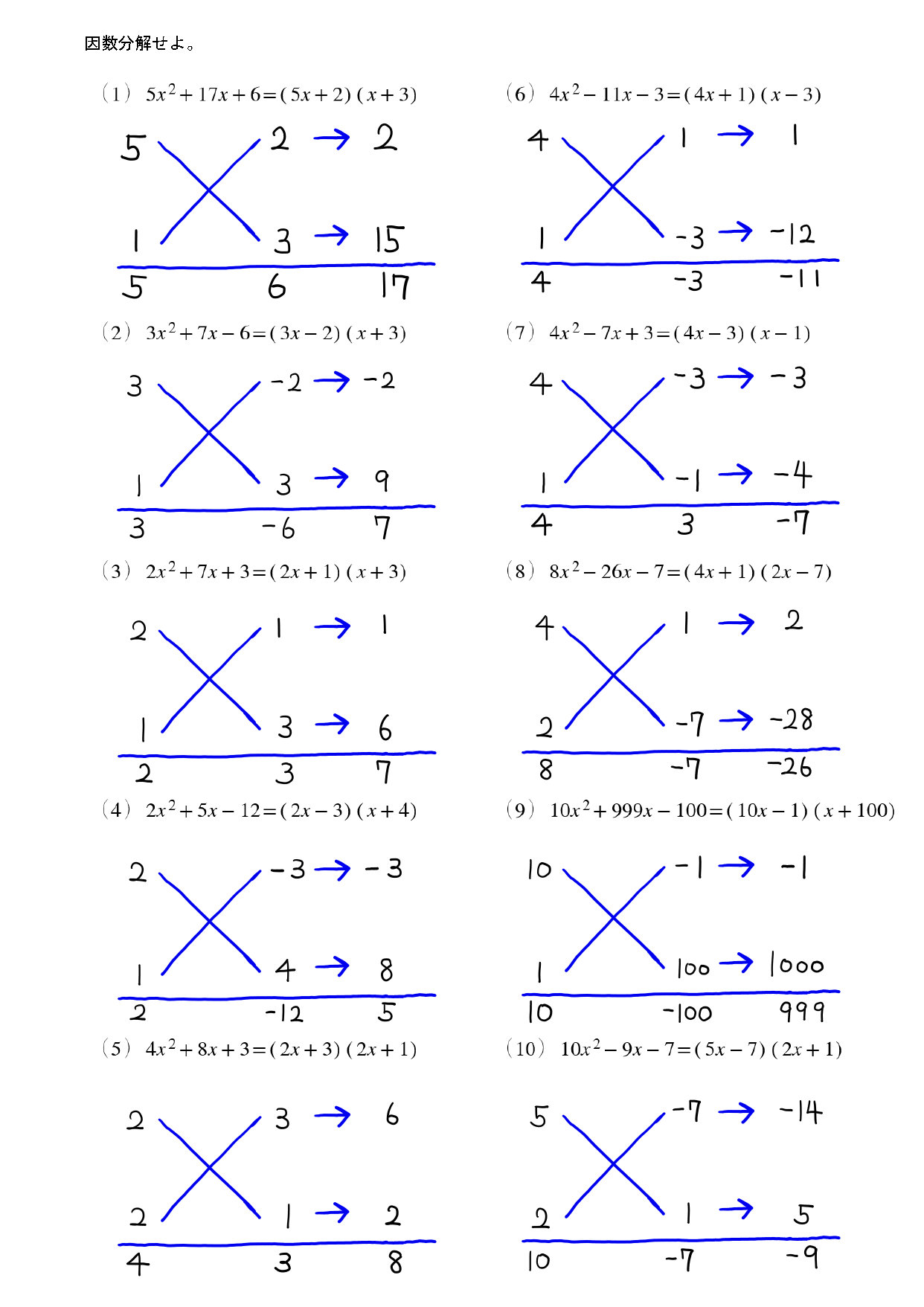
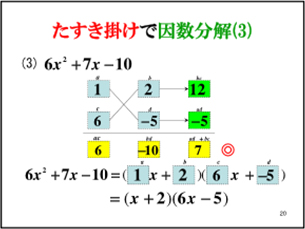
「たすきがけ」を使う因数分解、答えを もっと早く見つけて解く方法 が知りたい! 高校数学Ⅰの因数分解の「たすき掛け」、候補の数字がたくさんあると、どれが正しい組み合わせかを見つけるまで何度も「たすき掛け」することになってしまって大変だよね。因数分解は「たすきがけ」を使うと機械的にとけます。前述の問題も、「たすきがけ」を使えば難しく無いです。たすき掛けで因数分解する場合、両端の項に注目します。 x 2 と1は、何の数(文字)の積になるか考えてください。すると たすき掛け因数分解 (基) 公式:acx 2 (adbc)xbd= (axb) (cxd)をつかう。 これはxの係数11とはあわない。 これはxの係数11と一致する。 x2の係数が12なので、積が12になるような1×12,2×6, 3×4をaとcにあてはめ、 さらに積が定数項の15になるような1×15,3×5をbとdに入れ、たすき掛けして和が11になるような組み合わせを探す。




因数分解の問題なのですが 途中の Y 4 Xはどこへ行ったのでしょうか Clear




数学 問題演習 たすき掛けを用いる因数分解 教科書より詳しい高校数学
因数分解 たすき掛け 斜めに掛け算するとこんな感じ👇 因数分解 たすき掛け そして、掛け算して出てきた答えを足しましょう。 32=5 ですね。 この数字が1乗の項の係数になっていればたすき掛け成功です。 因数分解 たすき掛け もし、ここで1乗の動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 因数分解の問題です。 因数分解に慣れてきたこの子は、 式の形を見ています。 2 次 3 項式と呼ばれる形の因数分解です。 「 」は、2 次の項です。 「 」は、1 次の項です。 「 」は、 0 次の項(定数項)です。 このように、 2 次で、 3 つの項ですから、




因数分解 失敗しないたすき掛け ほぼ一発 Youtube




高校の因数分解公式一覧 たすき掛けや手順 やり方
数1因数分解 たすき掛け 数1因数分解 たすき掛け整数分解工具计算一个给定的自然数的质因数,也可以使用带 * / ^ !分 解质 因数 bai 的方法有 du 两种 : 1、相 乘法 写成几个质 zhi 数相乘的 dao 形式(这些不 版 重 复的 质数即 为质 权 因数),实际运算时可采用逐步分解的方式。たすきがけによる因数分解 ポイント 高校数学の第一のハードルがこの「たすきがけによる因数分解」です。 結局はただの計算技術です。難しく考えないで、ただひたすら練習しましょう。 たすきがけ たすきがけの因数分解とは、 \(



たすき掛けのやり方を徹底解説 因数分解の計算問題 受験辞典




高校数学 たすき掛けの因数分解 数樂管理人のブログ




たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com




たすきがけの因数分解のやり方 問題付き 理系ラボ



因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方




たすき掛けのやり方 因数分解がスラスラ解けるようになる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com




たすきがけの因数分解のやり方 問題付き 理系ラボ




たすき掛けのやり方 因数分解がスラスラ解けるようになる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




スーパーたすきがけ 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 因数分解公式と3次式の因数分解 受験の月




数学克服アドバイザー Sur Twitter 因数分解についての質問を受けました 許可を頂いたのでその解説を公開します 参考にして下さい ノートに書いて復習すれば効果的なのでぜひ 気軽にdmで質問して下さい 数学 数ii 因数分解 たすき掛け



数学高校一年生 因数分解の応用です イコールの三つ目あたりから Yahoo 知恵袋



高一です 因数分解のこのたすき掛けのやり方って数が大きくなったらすご Yahoo 知恵袋



超簡単な因数分解 たすき掛け でバッチリ テスト対策特別授業無料 完全1対1 マンツーマン 個別指導塾 家庭教師 福島県郡山市のプロ家庭教師 高校受験 大学受験対策 成績アップのお手伝い 小学生 中学生 高校生 文系 全ての学年指導可能 駿英家庭教師学院の
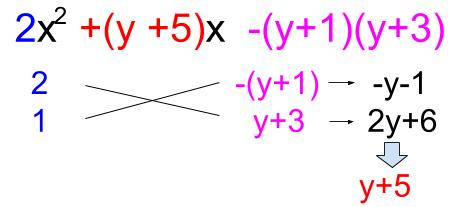



複雑なたすき掛け因数分解 高校数学の無料オンライン学習サイトko Su




たすきがけの因数分解のやり方 問題付き 理系ラボ




添削課題 数と式 横浜市立大 因数分解 教科書流とスーパーたすき掛けで 5月9日追記 Matsu Math Note
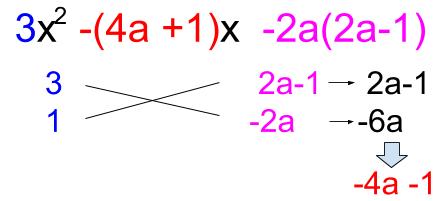



複雑なたすき掛け因数分解 高校数学の無料オンライン学習サイトko Su




たすきがけの因数分解のやり方 問題付き 理系ラボ
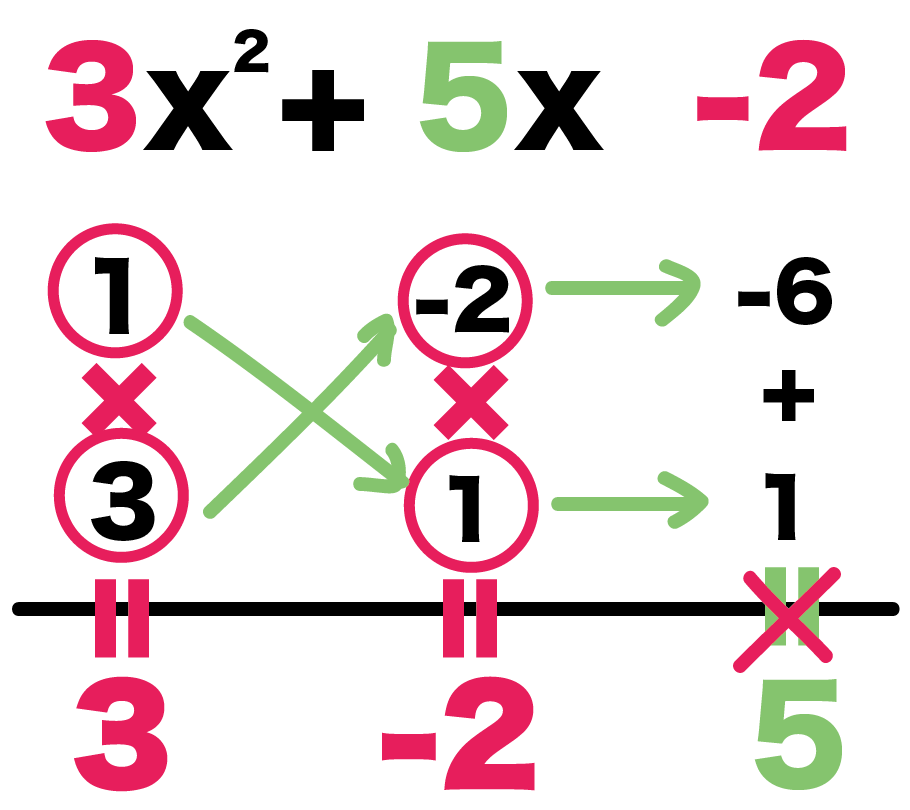



中学数学 たすき掛け因数分解のやり方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく



1




たすき掛けのやり方 因数分解がスラスラ解けるようになる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




たすき掛けで因数分解をするやり方を解説 これでたすき掛けに困らない




高校数学 A 因数分解のたすき掛けを一発で求めるコツ やはり俺の考察ブログはまちがっている アニメ 数学




たすきがけの因数分解のやり方 問題付き 理系ラボ
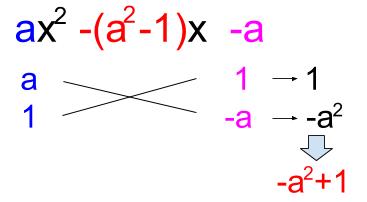



たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com



高卒認定試験の対策 過去に高認数学で出題された因数分解のたすきがけ問題の対策 坂田先生のブログ オンライン家庭教師の数学講師



たすき掛けのやり方を徹底解説 因数分解の計算問題 受験辞典



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ



Q Tbn And9gcrkj1p6dyqc9iaz Goofqjsryy Ve0sfvgyjajvgxa Usqp Cau




たすき掛けのやり方 因数分解がスラスラ解けるようになる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




因数分解の方法 公式と問題のまとめ たすき掛けや応用的なコツも解説




たすき掛けで因数分解をするやり方を解説 これでたすき掛けに困ら



因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方




高校数学 複数の文字を含む因数分解は最も次数が低い文字で整理せよ 受験の月



因数分解のたすき掛けで 画像のように左右の掛け合わせる数が複 Yahoo 知恵袋




高校数学 2次3項式ax Bx Cの因数分解 たすき掛け 受験の月




数i因数分解 難しいたすき掛け Youtube




たすき掛けの因数分解が苦手な人へ 簡単に解くための3つのコツ オンラインスクールカウンセリング寺子屋
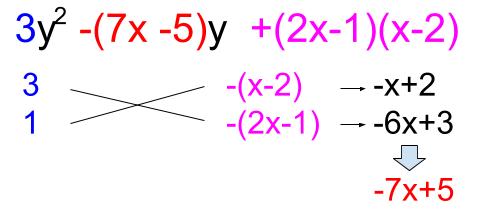



複雑なたすき掛け因数分解 高校数学の無料オンライン学習サイトko Su




数 たすき掛けの因数分解 Education Unbeatable




数学i 因数分解 たすき掛けの方法を紹介 高校数学 数i 因数分解 たすき掛け Youtube




数学iの因数分解について質問です Clear
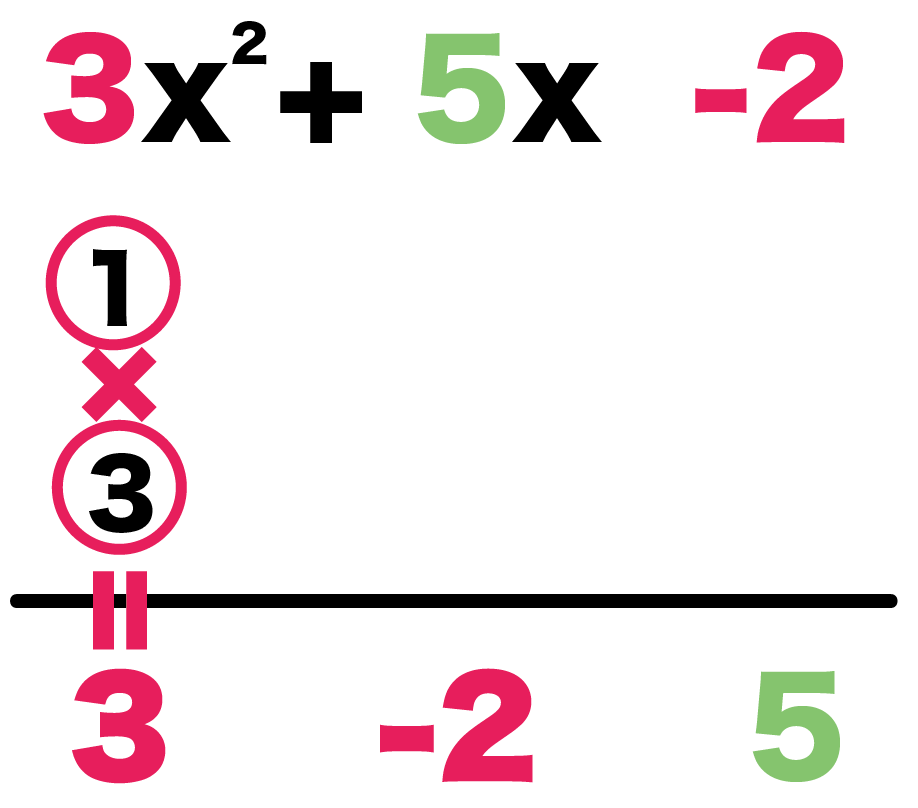



中学数学 たすき掛け因数分解のやり方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




高校数学 数 勉強動画 因数分解 たすき掛け編の問題 19ch
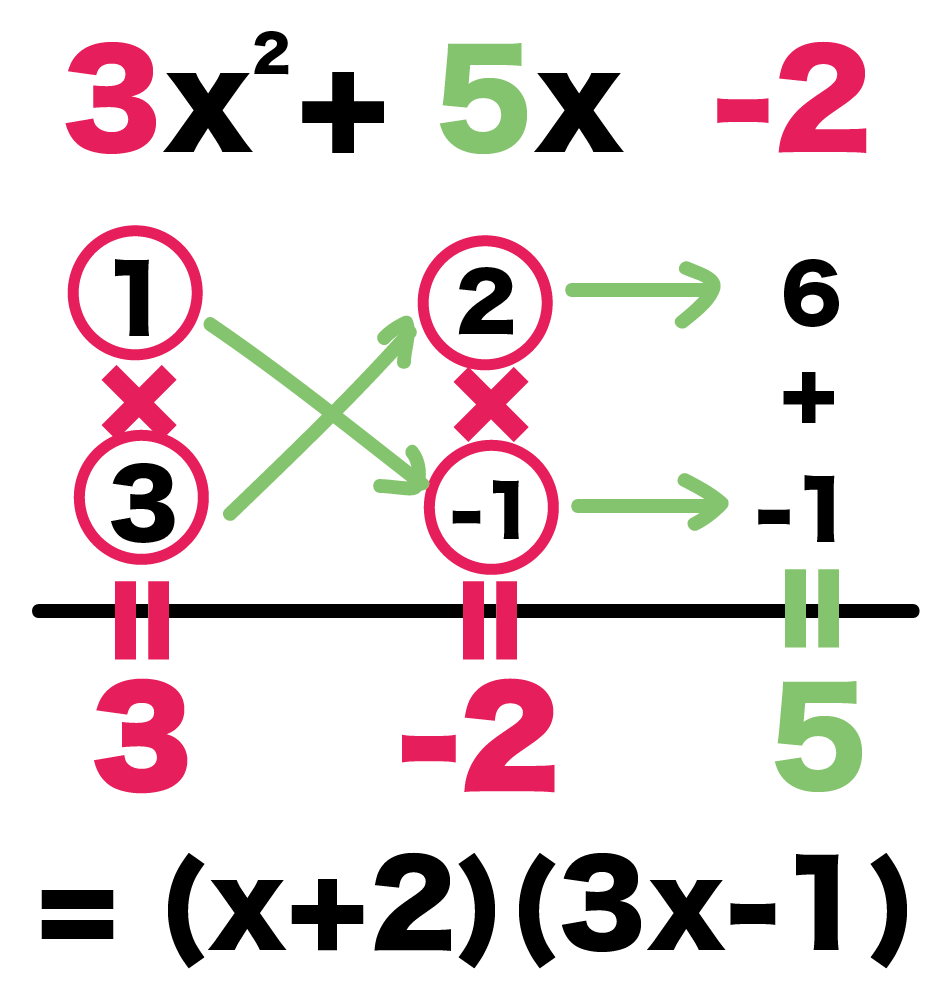



中学数学 たすき掛け因数分解のやり方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




高校数学 数 第1章 数と式 6 因数分解 たすき掛け 壱のblog



2文字のたすき掛け




因数分解たすきがけの裏ワザ 教科書では教えてくれない たすき掛けを早く簡単にする方法 とは 教科書をわかりやすく通訳するサイト




高校数学 たすき掛けの因数分解 数樂管理人のブログ




因数分解の見分け方と仕組みについて 因数分解の見分け方を教えて下さい Okwave




たすき掛けの因数分解が苦手な人へ 簡単に解くための3つのコツ オンラインスクールカウンセリング寺子屋



たすき掛け因数分解
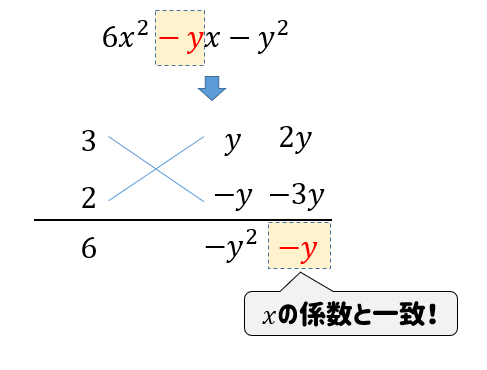



たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ




たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com




高校数学 数 9 因数分解 たすき掛け編 Youtube




たすき掛けによる因数分解のコツとは 大学入試数学の考え方と解法




因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する
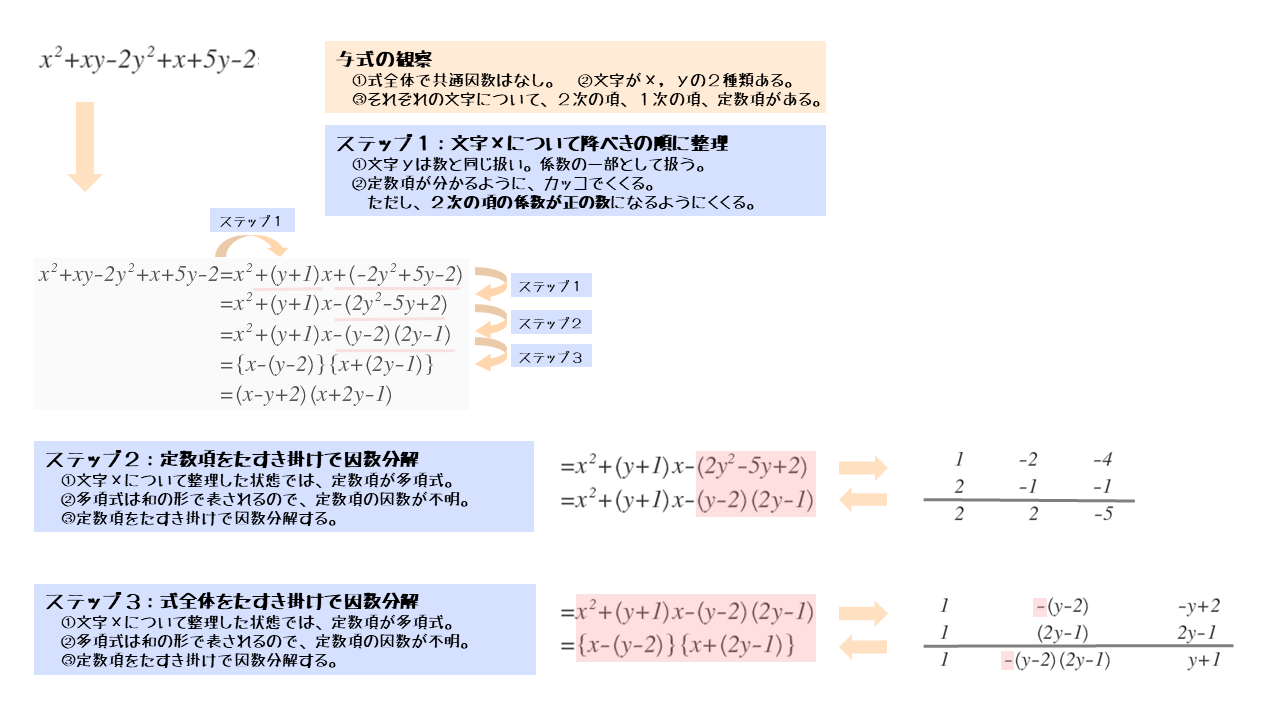



数と式 整式をたすき掛けで因数分解してみよう 日々是鍛錬 ひびこれたんれん
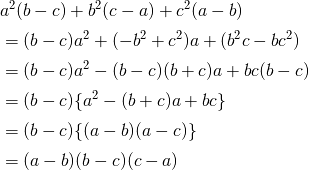



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局



中学高校数学 たすきがけ 因数分解 の裏ワザ 東大 桐生雄大 Note



授業実践記録 数学 併設型中高一貫教育校で行った先取り学習の授業発表会 ちょっと複雑な因数分解 たすき掛け 啓林館



1




たすき掛けのやり方 因数分解がスラスラ解けるようになる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学 たすきがけを使う因数分解 映像授業のtry It トライイット
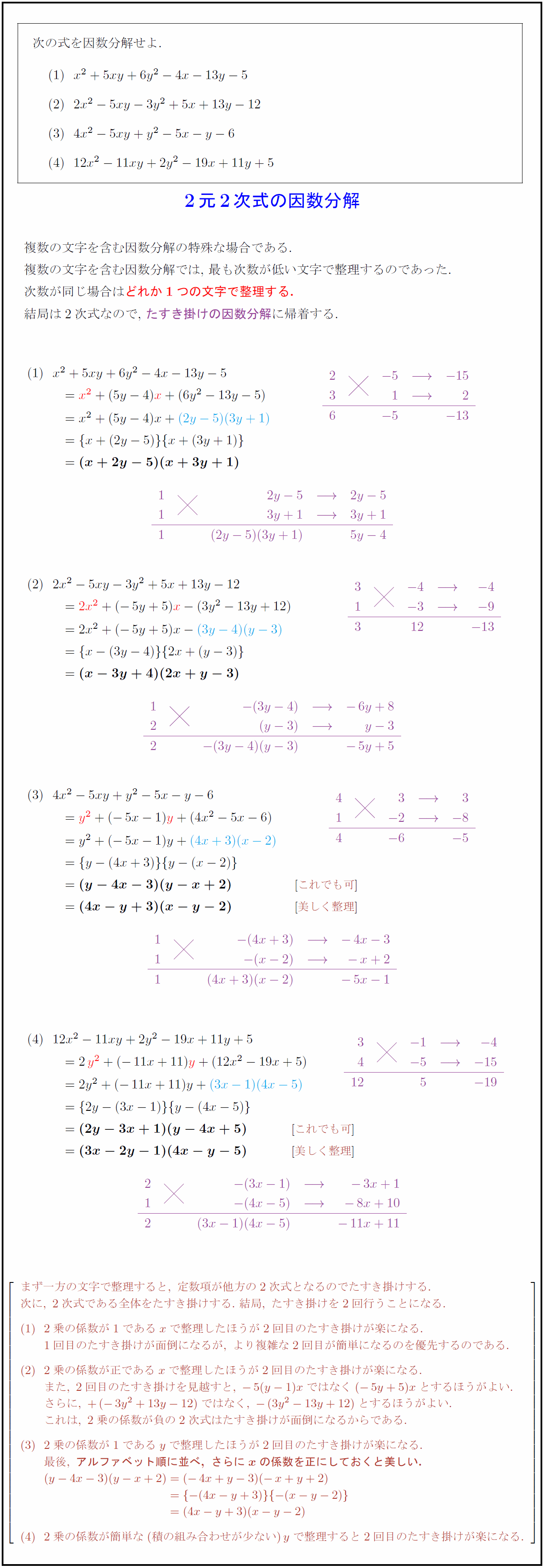



高校数学 2元2次6項式ax Bxy Cy Dx Ey Fの因数分解 受験の月



たすきがけのやり方について 数学 苦手解決q A 進研ゼミ高校講座




因数分解 2 たすきがけの思考手順 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 因数分解のたすきがけ問題を早く解くコツは どんなたすきがけもラクラク




高校数学 A 因数分解のたすき掛けを一発で求めるコツ やはり俺の考察ブログはまちがっている アニメ 数学




たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com



たすきがけのやり方について 数学 苦手解決q A 進研ゼミ高校講座




高校数学 因数分解のたすきがけ問題を早く解くコツは どんなたすきがけもラクラク
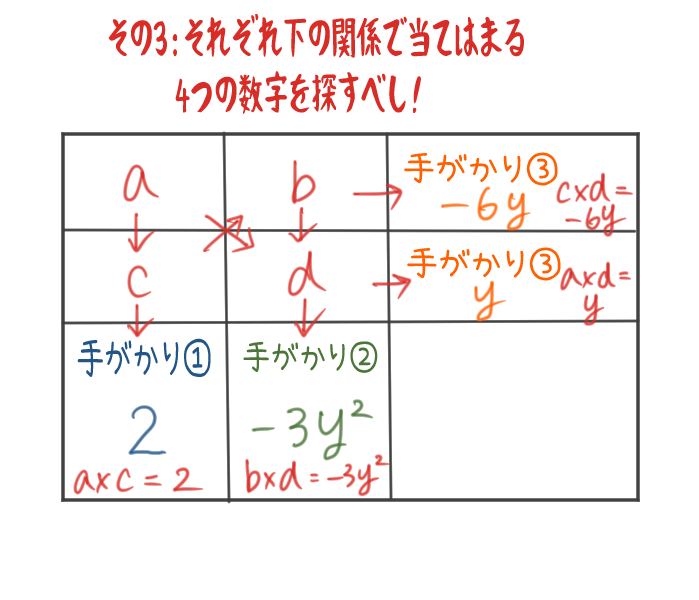



因数分解たすきがけの裏ワザ 教科書では教えてくれない たすき掛けを早く簡単にする方法 とは 教科書をわかりやすく通訳するサイト




数と式 整式をたすき掛けで因数分解してみよう 日々是鍛錬 ひびこれたんれん




高校数学 たすき掛けの因数分解 数樂管理人のブログ
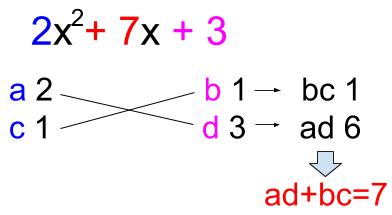



たすきがけの因数分解 高校数学の無料オンライン学習サイトko Su



たすき掛け因数分解




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト
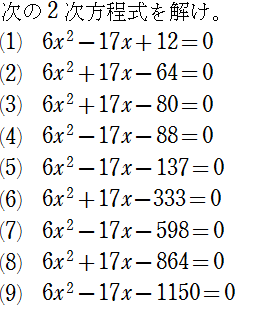



因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 数 10 因数分解 応用編 Youtube




因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する



1




因数分解 2 たすき掛け 数 宇宙を歩く高校数学 基礎
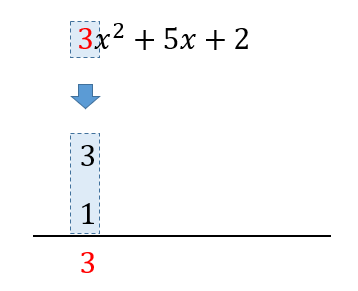



たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ




数学i 因数分解1 たすき掛け ゼロから始める高校数学 第5講 Youtube




数学ia 因数分解の難問も簡単に解ける計算のやり方 たすき掛けも解説 Himokuri



0 件のコメント:
コメントを投稿